Classical Mechanics

A point-like object of mass $m$ is travelling around the origin of the coordinate system in a circle of radius $R$ within the $xy$-plane.

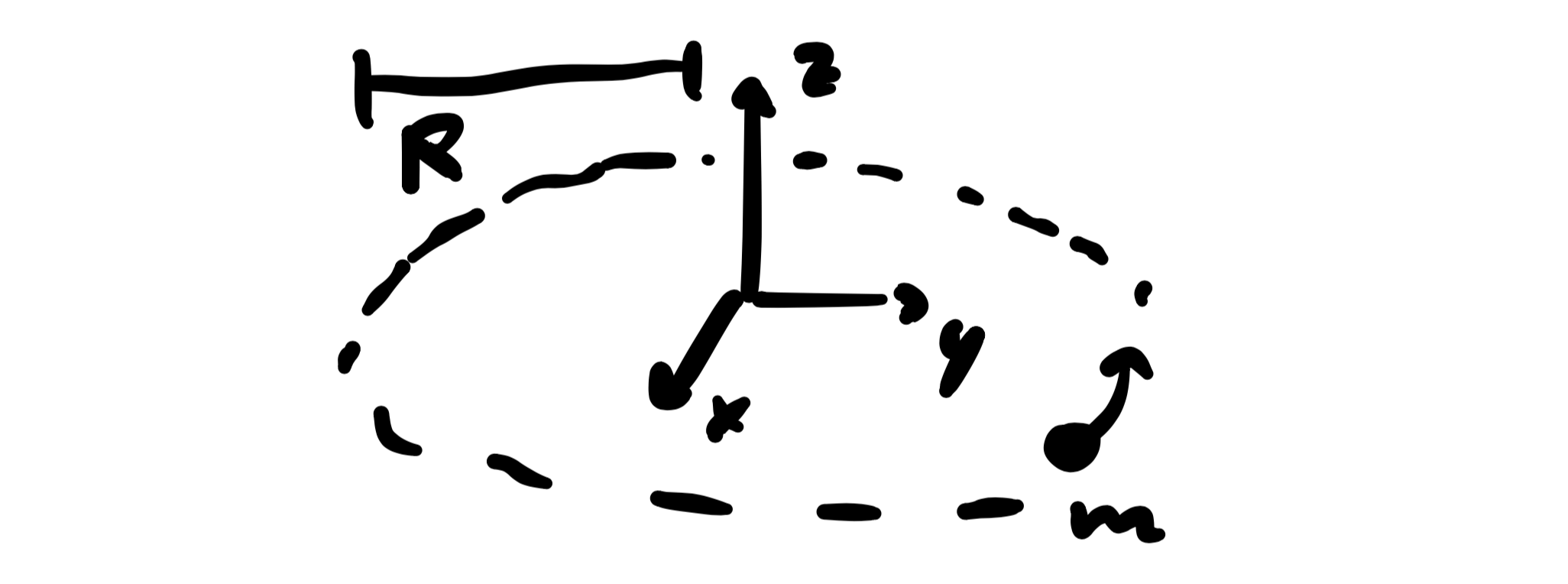
Calculate the point's moment of inertia for this motion!   Hint

The moment of inertia is given by $I = \int r_\perp^2 \text dm$.

A rod of length $L$, negligible width and height ($h\ll 1$, $w\ll 1$) and constant density $\rho$ is rotating around a fixed axis.

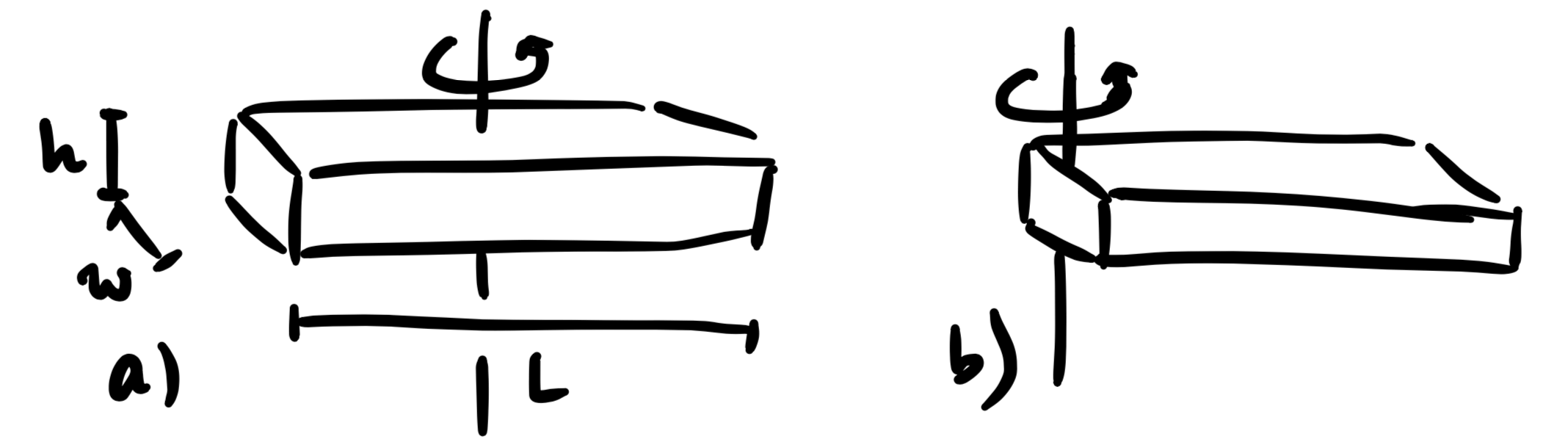
1. Calculate the rod's moment of inertia for a rotation around an axis through the center of mass!   Hint

   The moment of inertia is given by $I = \int r_\perp^2 \text dm$.

2. Calculate the moment of inertia for a rotation around one end of the rod!   Hint

   Use the parallel axis theorem.

A disk of radius $R$, height $h$ and constant density $\rho$ is rotating around a fixed axis.

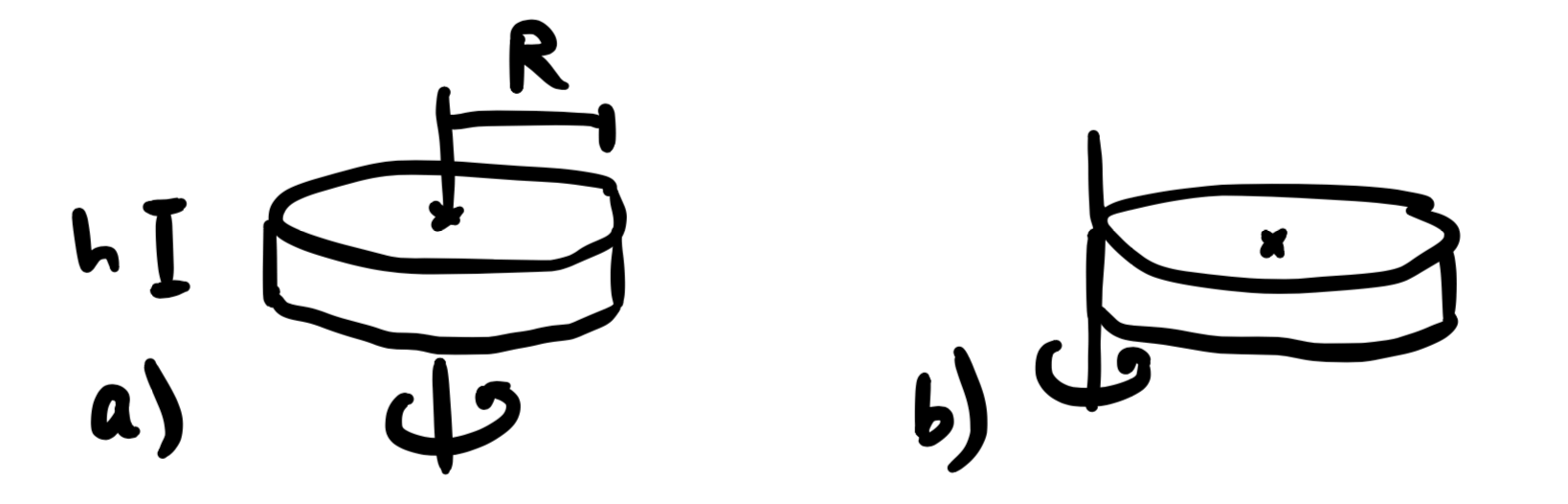
1. Calculate the disk's moment of inertia for a rotation around an axis through the center of mass perpendicular to the disk!   Hint

   The moment of inertia is given by $I = \int r_\perp^2 \text dm$.

2. Like (a) but move the axis of rotation to the boundary of the disk!   Hint

   Use the parallel axis theorem.

The Lagrangian of a system is given by $L(q_i,\dot q_i)=T-V$, where $T$ is the kinetic energy and $V$ is the potential energy and $q_i$ are generalized coordinates for $N$ degrees of freedom $(i=1\ldots N)$.

Use the principle of least action to derive the Euler-Lagrange Equations for this system!   Hint

The principle of least action states that a system will behave in such a way that the action, $$S = \int \text dt\,L(q_i, \dot q_i) ,$$ takes on an extremal value: $\delta S = 0$.

Solution  

The Lagrangian density of a system is given by $\mathcal L(\varphi_i,\partial_\mu \varphi_i)$, where $\varphi_i(x^\mu)$ are the fields that correspond to $N$ degrees of freedom $(i=1\ldots N)$.

Use the principle of least action to derive the Euler-Lagrange Equations for this system!   Hint

The principle of least action states that a system will behave in such a way that the action, $$S = \int\text d^4x\, \mathcal L(\varphi_i,\partial_\mu \varphi_i) ,$$ takes on an extremal value: $\delta S = 0$.

Solution  

The Hamiltonian of a system is given by $H(q_i,p_i)=T+V$, where $T$ is the kinetic energy and $V$ is the potential energy and $q_i$ are generalized coordinates for $N$ degrees of freedom $(i=1\ldots N)$.

Use the definition of the Hamiltonian as the Legendre transformation of the Lagrangian to derive Hamilton's equations of motion!   Hint

The Hamiltonian is given by $H(q_i,p_i) = \sum\limits_i p_i \dot q_i -L(q_i, \dot q_i)$.

Solution  

The Hamiltonian for a free, non-relativistic particle is given by $H(q,p) = \frac{p^2}{2m}$, where $m$ is the particle's mass.

1. Apply Hamilton's equations of motion for this system to get two differential equations!

2. Solve these equations!

Solution